Realimentação positiva: algo importante, mas que pouco ouvimos falar.

Neste post discutiremos o que é a realimentação positiva, qual a relação com a realimentação negativa e com sistemas instáveis.

Nos próximos posts falaremos sobre comparadores Schmitt-trigger e como eles utilizam realimentação positiva.

Realizaremos uma análise básica sobre realimentação positiva. Para uma discussão completa sobre o assunto recomendo livros sobre controle de sistemas lineares, como Livro: Engenharia de Controle Moderno (Ogata). Veja outros livros sobre controle em Categoria: Livros de controle.

Inscreva-se em nossa lista de emails para ser avisado sobre novos posts em resumos semanais.

Realimentação positiva

No post Teoria: Realimentação (Feedback) vimos que realimentação consiste em amostrar a saída de um sistema e subtrair (ou somar) parte desta amostra no sinal de entrada.

Dependendo da operação realizada com o sinal amostrado da saída (subtrair ou somar) obtemos realimentação negativa ou positiva. Podemos ver que no post acima o sinal que passa pelo bloco H é subtraído do sinal de entrada, enquanto neste post o sinal é somado, caracterizando os dois tipos de realimentação.

Podemos obter a equação do ganho realimentado a partir da equação abaixo (mesmo método que no post sobre realimentação).

Na equação do ganho realimentado a diferença entre realimentação negativa e positiva é simplesmente o sinal de mais+ ou menos- antes de GH. (¡¡¡ Note que realimentação NEGATIVA tem o sinal mais+ e realimentação POSITIVA tem o menos- !!!)

Na prática os dois tipos de realimentação tem funções completamente diferentes.

A realimentação negativa atua de forma a atenuar o sinal de entrada no amplificador, para controlar o ganho do sistema de acordo com o ganho de realimentação (bloco H).

A realimentação positiva, por sua vez, reforça o sinal de entrada no amplificador. Isso pode causar duas coisas: aumentar o ganho do amplificador realimentado; ou tornar o amplificador instável.

Sistemas estáveis e instáveis

Aqui é onde entra o estudo de controle de sistemas!

(É preciso deixar claro que a partir daqui estamos discutindo o modelo matemático do sistema, não o sistema em si. Veremos nos posts sobre comparadores Schmitt-trigger que, mesmo sendo um sistema instável, a saída não vai para o infinito.)

Em sistemas estáveis a saída será estável se a entrada for estável. Ou seja, se a entrada não ir para ±infinito a saída também não vai. Isso, por exemplo, é perfeito para amplificadores e controle de sistemas.

Já em sistemas INSTÁVEIS o mesmo não acontece! Não importa o que há na entrada, pode ser instável, estável ou zero… a saída vai tender a ±infinito. A saída pode tender a +infinito, a -infinito ou oscilar com aplitude tendendo ao infinito.

Ao projetar um controlador de um sistema queremos ficar LONGE da instabilidade! Por isso precisamos conhecer o que é e como funciona realimentação positiva: pois ela está a um passo da instabilidade. E há técnicas para determinar o quanto o sistema está longe da instabilidade (margem de ganho e margem de fase).

Sistemas estáveis com realimentação positiva

Um sistema é estável enquanto o denominador da equação de ganho realimentado é positivo (maior que zero, mas não igual a zero).

Veja que quando o sistema está configurado com realimentação positiva será difícil manter a estabilidade, pois os valores estáveis de GH são bastante restritos.

A equação de ganho é inválida para sistemas instáveis

Mas porque o sistema é estável somente enquanto o denominador da equação de ganho realimentado é positivo?

Isso deve-se ao fato da equação de ganho realimentado é inválida para sistemas instáveis!

Vejamos o gráfico abaixo (código no fim do post). Em primeiro lugar, para a geração do gráfico consideramos H=1. No gráfico vemos o ganho do amplificador G crescendo de 0 até 2.

Com G indo de 0 até 1 vemos o ganho do sistema ir de zero até tender a +infinito. Nesta parte, exceto quando G=1 o sistema é estável (sistema estável se ).

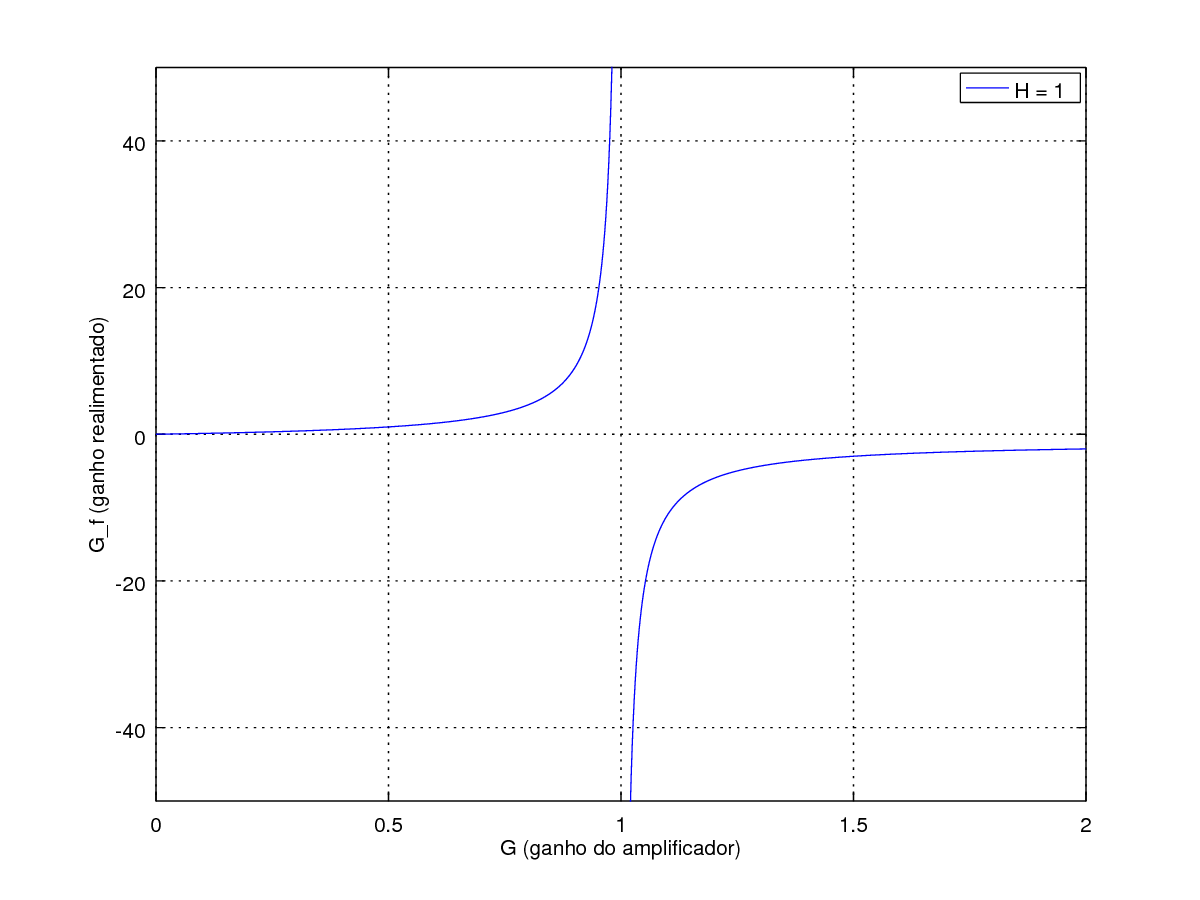
Veja que o quando G=1 o ganho Gf vai para o +infinito e logo depois é negativo, vindo do -infinito! É neste ponto que o sistema se torna instável e a equação de ganho realimentado não é mais válida.

Note a contradição entre o ganho realimentado e o comportamento do sistema:

Ganho realimentado:
* Considerando G=2 e H=1;
* Gf = G/(1-GH) = -2

Comportamento do sistema:
* Considerando G=2 e H=1;
* Coloque o sinal vi0=1 na entrada,
* Teremos o sinal 2 [vi0 G] na saída,
* Teremos o sinal 2 [vi0 G H] na realimentação somando com vi,
* Teremos o sinal 6 [(vi0 + (vi0 G H)) G] na saída,
* Teremos o sinal 6 [(vi0 + (vi0 G H)) G] na realimentação somando com vi,
* Teremos o sinal 14 [(vi0 + (vi0 + (vi0 G H)) G) G] na saída,
* E assim por diante…

O ganho Gf é negativo e o sinal de saída do sistema é positiva para entrada positiva!!! (?)

O que aconteceu com a matemática???!!!

Contradições geralmente revelam que algo não está sendo tratado corretamente.

Neste caso, a equação de ganho realimentado Gf é válida apenas quando o sistema é linear. E, a partir do momento que o ganho G passou pelo valor 1, o sistema não é mais linear!

Exatamente! O sistema se torna exponencial instável.

De forma direta: a equação e o uso dela não faz mais sentido assim que o denominador (1 – GH) torna-se zero.

É precisamente isso que tentamos evitar ao realizar a análise de estabilidade e controle de um sistema.

Aplicações

Mas não simplifique demais as coisas: realimentação positiva não é algo que deve-se fugir a vida toda!

Há aplicações onde ela é essencial ou, no mínimo, muito importante. Algumas aplicações são:

– Osciladores
– Comparadores com histerese (Schmitt-trigger)

Fique ligado para não perder os próximos posts, onde veremos comparadores Schmitt-trigger.

Código para o gráfico

Este é o código MATLAB/OCTAVE para gerar o gráfico.

% MATLAB/OCTAVE
% Código para gerar o gráfico de ganho com realimentação
%   positiva com ganho de amplificador variando
%   Gf = G/(1-GH) vs G

H = 1;
G = (0 : 0.001 : 2);

Gf = G./(1 - G .* H);

plot(G,Gf)
xlabel('G (ganho do amplificador)')
ylabel('G_f (ganho realimentado)')
legend({['H = ', num2str(H)]})
grid on
xCenter = 1/H;
xDiff = (max(G)-min(G))/2;
axis([xCenter-xDiff xCenter+xDiff -50 50])

Compartilhe!

Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!

Veja mais posts sobre Teoria.