AMPOP inversor e realimentação

Hoje veremos o AMPOP na configuração inversora, um exemplo mais complexo sobre AMPOPs e realimentação.

Este é nosso terceiro post da série sobre realimentação. Se não viu, recomendo os posts anteriores Teoria: Realimentação (Feedback) e Teoria: AMPOP não-inversor e Realimentação (Feedback).

Não se esqueça de se inscrever em nossa lista de emails para ser avisado sobre novos posts em resumos semanais.

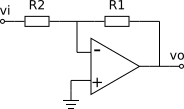
Na configuração inversora, mostrada acima, o raciocínio é um pouco mais complicado que na configuração não-inversora, pois além de serem utilizados na malha de realimentação (H = vin/vo), os resistores R1 e R2 também geram um divisor resistivo na tensão de entrada (Gi = vin/vi).

Note que a tensão de entrada negativa (vin) depende de ambos a entrada (vi) e a saída (vo).

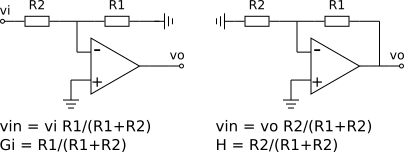
Como podemos ver na imagem acima, para a entrada vi é como se o resistor R2 estivesse aterrado, gerando um divisor resistivo (ganho de entrada Gi = vin/vi). Para a saída vo é como se o resistor R1 estivesse aterrado, gerando outro divisor resistivo (ganho de realimentação H = vin/vo).

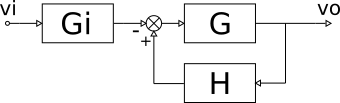
Portanto, o sistema realimentado que representa um AMPOP inversor é constituído por um ganho de entrada (Gi) e o AMPOP realimentado, como mostra a imagem acima. Note que, como o sinal de entrada vi influencia na entrada inversora do amplificador operacional, o sinal correspondente no sistema a entrada vi é negativo e o sinal de realimentação é positivo.

Utilizando a equação de realimentação obtemos Gf (correspondente apenas ao AMPOP realimentado), onde G é o ganho do AMPOP e H é o ganho de realimentação. O sinal negativo é devido a configuração inversora, o mesmo motivo dos sinais de entrada e de realimentação terem os sinais trocados no diagrama de realimentação.

O ganho ainda não se parece com o que estamos acostumados para a configuração inversora. Para isso precisamos multiplicar pelo ganho da entrada Gi e obter o ganho total Gt do amplificador inversor.

Assim, se G for muito maior que 1, ou seja, G >> 1, o termo 1 / G tenderá a zero e não influenciará significativamente no ganho total.

E este é o ganho que estamos acostumados a ver quando se trata de AMPOPs inversores.

Utilizando equações

Podemos obter o mesmo resultado a partir das equações do ganho G do AMPOP, da tensão vin em função das tensões de entrada e de saída e considerando que vip = 0 (aterrado).

Compartilhe!

Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!

Veja mais posts sobre Teoria.