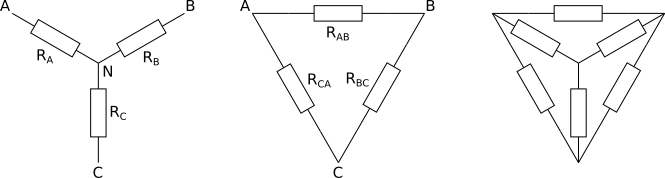
Além de estar em série ou paralelo, resistores podem também estar formando uma estrela (ípsilon Y, tê T) ou um triângulo (delta Δ, pi Π).
Algumas vezes não é possível simplificar o circuito com apenas paralelo e série, sendo necessário realizar uma transformação estrela-triângulo ou triângulo-estrela.
Veja também como programar sua calculadora HP50g para calcular as transformações estrela-triângulo e triângulo-estrela!
Veja a lista de posts do Curso Circuitos Elétricos em sequência.
Resistores ligados em estrela em triângulo
Um conjunto de resistores ligados em estrela possui três terminais externos A, B, C e um terminal interno N.
Um conjunto de resistores ligados em triângulo possui os mesmos três terminais externos A, B, C e nenhum terminal interno.
A transformação estrela-triângulo de resistores busca um circuito equivalente em triângulo que seja idêntico ao circuito em estrela.
Da mesma forma, a transformação triângulo-estrela de resistores busca um circuito equivalente em estrela que seja idêntico ao circuito em triângulo.

Transformação triângulo-estrela ∆→Y
Começamos transformando resistências de triângulo para estrela.
Quando medimos a resistência entre os terminais A e B de ambos triângulo e estrela, para serem equivalentes eles devem medir a mesma resistência. O mesmo é válido para os outros dois pares de terminais.
Assim obtemos as seguintes equações, onde || significa operação de paralelo de resistências e definimos R∆ como a soma das três resistências delta.
RA+RB = RAB||(RBC+RCA) = RAB(RBC+RCA)/R∆
RB+RC = RBC||(RCA+RAB) = RBC(RCA+RAB)/R∆
RC+RA = RCA||(RAB+RBC) = RCA(RAB+RBC)/R∆
R∆ = RAB+RBC+RCA
Subtraindo a segunda equação da primeira obtemos o seguinte.
RA-RC = RCA(RAB-RBC)/R∆
Somando esta equação com a terceira equação e dividindo por 2 obtemos a equação para RA e por consequência obtemos RB e RC.
RA = RABRCA/R∆
RB = RBCRAB/R∆
RC = RCARBC/R∆
R∆ = RAB+RBC+RCA
Assim concluímos que RA, a resistência equivalente Y do terminal A, é igual a multiplicação das resistências ∆ adjacentes a ela RABRCA dividido pela soma das três resistências ∆ RAB+RBC+RCA. As outras duas resistências são análogas.
Transformação estrela-triângulo Y→∆
Da Lei de Kirchhoff das tensões entre os nós C, N do circuito Y obtemos a seguinte equação. Consideramos todas as correntes entrando no terminal na direção de N e RY = RA||RB||RC.
VN = VC-ICRC = VC+VARC/RA+VBRC/RB-VNRC/(RA||RB)
VN = RY(VA/RA+VB/RB+VC/RC)
RY = RA||RB||RC
Calculando as correntes do circuito Y obtemos as seguintes correntes.
IA = (VA-VN)/RA = VA(1/RA-RY/RA2)-VBRY/RARB-VCRY/RARC
IB = (VB-VN)/RB = -VARY/RARB+VB(1/RB-RY/RB2)-VCRY/RBRC
IC = (VC-VN)/RC = -VARY/RARC-VBRY/RBRC+VC(1/RC-RY/RC2)
Da Lei de Kirchhoff das correntes nos nós A, B, C do circuito ∆ obtemos as seguintes equações. Consideramos as correntes dos resistores indo de A para B, de B para C e de C para A.
IA = IAB – ICA = VA/(RAB||RCA)-VB/RAB-VC/RCA
IB = IBC – IAB = -VA/RAB+VB/(RAB||RBC)-VC/RBC
IC = ICA – IBC = -VA/RCA-VB/RBC+VC/(RBC||RCA)
Como ambos os circuitos são equivalentes um do outro, é necessário que as correntes sejam iguais. Portanto cada termo correspondente a uma das entradas deve ser igual nas duas equações. Com facilidade podemos usar IA para determinar RAB e RCA e usar IB para determinar RAB e chegar a conclusão abaixo.
RAB = RARB/RY
RBC = RBRC/RY
RCD = RCRA/RY
RY = RA||RB||RC
Assim concluímos que RAB, a resistência equivalente ∆ entre os terminais AB, é igual a multiplicação das resistências Y adjacentes a ela RARB dividido pelo paralelo das três resistências Y RA||RB||RC. As outras duas resistências são análogas.
Note que tanto as equações como o algoritmo são muito parecidos com a transformação triângulo-estrela!
Alguns livros trazem as equações a seguir, que são consequência das equações acima. Também há outra forma menos intuitiva de chegar diretamente nas e equações abaixo a partir das equações de triângulo para estrela, que não discutiremos aqui.
RAB = (RARB+RBRC+RCRA)/RC
RBC = (RARB+RBRC+RCRA)/RA
RCA = (RARB+RBRC+RCRA)/RB
Calculando transformação estrela-triângulo na HP50g
Caso esteja interessado em aprender a programar a calculadora HP50g veja nosso Curso Calculadora HP50g.
Neste ponto você já deve ter entendido o básico de como programamos na HP50g e de como usar os programas nos modos RPN e algébrico. Se não for o caso, revise as aulas sobre a) Resistência equivalente série e paralelo, b) Divisor de tensão e c) Divisor de corrente, onde temos a explicação passo-a-passo de como criar aqueles programas. Agora vamos direto aos programas!
Programa triângulo para estrela
Para simplificar o programa utilizamos quatro variáveis globais. Logo no início do programa colocamos o valor zero na pilha para ser lido junto com as resistências ∆. Na segunda linha calculamos o valor de R∆ e guardamos na variável Rd, que foi inicializada com zero. As outras três linhas calculam os valores de RA, RB e RC.
« 0 → RAB RBC RCA Rd « 'RAB+RBC+RCA' EVAL 'Rd' STO 'RAB*RCA/Rd' EVAL 'RBC*RAB/Rd' EVAL 'RCA*RBC/Rd' EVAL » »
Guarde este programa com nome “∆→Y” (a flecha e o delta podem ser encontrados no menu de caracteres [┌→][EVAL]).
Programa estrela para triângulo
Novamente, para simplificar o programa utilizamos quatro variáveis globais. Logo no início do programa colocamos o valor zero na pilha para ser lido junto com as resistências Y. Na segunda linha calculamos o valor de RY e guardamos na variável Ry, que foi inicializada com zero. As outras três linhas calculam os valores de RAB, RBC e RCA.
« 0 → RA RB RC Ry « '1/(1/RA+1/RB+1/RC)' EVAL 'Ry' STO 'RA*RB/Ry' EVAL 'RB*RC/Ry' EVAL 'RC*RA/Ry' EVAL » »
Guarde este programa com nome “Y→∆” (a flecha e o delta podem ser encontrados no menu de caracteres [┌→][EVAL]).
Compartilhe e deixe sua sugestão!
Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!
Veja a lista de posts do Curso Circuitos Elétricos.