Neste post falaremos sobre sistemas lineares, suas características e como identificá-los.
De forma simples, sistemas lineares são aqueles onde o princípio da superposição é válido. Mas não definimos ainda este princípio e mesmo assim queremos ser capazes de determinar se um sistema é linear ou não.
Veja a lista de posts do Curso Circuitos Elétricos em sequência.
Sinais, entradas e saídas
Sinais são as grandezas de interesse de um sistema. Nos sistemas da categoria “circuitos elétricos” (que estamos discutindo neste curso) os sinais mais utilizados são tensões elétricas e correntes elétricas.
Dessa forma, quando estamos analisando um circuito elétrico, estamos na verdade determinando os sinais de um sistema. Temos um circuito elétrico (sistema) e as diversas tensões e correntes nos elementos (sinais) que queremos determinar.
As entradas de um sistema são os sinais controlados através de algum meio externo. Nos circuitos elétricos os elementos que operam como entradas geralmente são as fontes de tensão e corrente independentes.
Saiba que fontes controladas/dependentes não são entradas; elas fazem parte da dinâmica interna do sistema!
As saídas de um sistema são os sinais de interesse, que desejamos medir. Nos circuitos elétricos as saídas geralmente também são tensões ou correntes nos elementos.
Sistemas lineares e não-lineares
Agora que temos uma noção básica de sistemas (o que são sinais, entradas e saídas), podemos discutir o que são sistemas lineares.
Os sistemas lineares são um grupo de sistemas muito importante na engenharia, pois possuem uma dinâmica matematicamente simples, havendo um conjunto de métodos e ferramentas muito poderosas de análise para esse tipo de sistema.
Sistemas não-lineares são mais complexos matematicamente, não havendo métodos protos capazes de analisar todos os sistemas não-lineares. Praticamente cada sistema não-linear exige uma estratégia própria de análise.
Os sistemas não-lineares podem, no entanto, ser linearizados em torno de um ponto de operação através da série de Taylor e ser analisados como um sistema linear quando operando próximo deste ponto de operação.
Os circuitos elétricos tratados neste curso são sistemas lineares com respeito a corrente e tensão. Portanto ou os elementos são todos lineares.
Sistemas lineares
Vamos tratar agora do que são sistemas lineares e como determinar se um sistema é linear ou não.
Um sistema é linear se ele possui a seguinte propriedade: a saída correspondente a soma de dois sinais de entrada é igual a soma das saídas correspondentes a cada sinal individual.
Sim, a frase é complicada. Vou explicar ele e em seguida relemos ela.
Em vez de falar de “sistemas” vamos falar diretamente de circuitos elétricos.

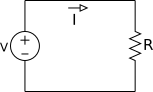
Consideramos o circuito elétrico linear acima. Onde temos uma tensão de entrada V e uma corrente de saída I.
Aplicando uma tensão V=V1 na entrada obtemos uma corrente I=I1 na saída.
Agora, aplicando outra tensão V=V2 na entrada obtemos outra corrente I=I2 na saída.
Como o sistema é linear, se aplicarmos na entrada a soma V=V3=V1+V2 obtemos na saída I=I3=I1+I2.
Resolvendo o circuito para os três casos temos o seguinte.
V1→I1=V1/R
V2→I2=V2/R
V3=V1+V2→I3=(V1+V2)/R=I1+I2
Esta terceira linha nos mostra que esse o circuito é mesmo linear.
Agora vamos rever a propriedade de um sistema linear: a saída correspondente a soma de duas entradas é igual a soma das saídas correspondentes a cada entrada individual.
Circuitos elétricos e sistemas não-lineares
Nem todos os sistemas baseados em circuitos elétricos são lineares.
Acabamos de ver que, considerando sistema formado pelo circuito anterior, a tensão V sendo a entrada do sistema e a corrente I no resistor R sendo a saída, o sistema é linear.
Agora, considere o sistema formado pelo mesmo circuito, a tensão V sendo a entrada do sistema, mas agora a saída sendo a potência P no resistor R. Mostre que este sistema não é linear. (Basta seguir passos semelhantes aos anteriores e concluir que P3≠P1+P2 quando V3=V1+V2.)
Variação das entradas no tempo
Acabamos de ver que nos sistemas lineares com sinais constantes, se a entrada V1 causa a saída I1 e se a entrada V2 causa a saída I2, então a entrada V3=V1+V2 causa a saída I3=I1+I2.
Isso também é válido para sinais de entrada que variam no tempo!
Imagine que sua fonte de tensão V1(t) seja 0 V, exceto por um intervalo de tempo de 1 s, onde a tensão é 1 V. Imagine agora que a fonte de tensão V2(t) seja 0 V, exceto por um intervalo de tempo de 2 s, onde a tensão é 2 V. Cada uma destas entradas gerará sua corrente de saída correspondente I1(t) e I2(t).
Agora considere o sinal de entrada V3(t)=V1(t)+V2(t), ou seja, 0 V exceto pelo intervalo de 1 s, onde a tensão é 3 V, e mais 1 s, onde a tensão é 2 V. Esta entrada gerará uma corrente de saída I3(t)=I1(t)+I2(t), de acordo com a propriedade citada.
V1(t)→I1(t)=V1(t)/R
V2(t)→I2(t)=V2(t)/R
V3(t)=V1(t)+V2(t)→I3(t)=[V1(t)+V2(t)]/R=I1(t)+I2(t)
Sistemas lineares e proporcionalidade
Novamente citamos a propriedade dos sistemas lineares:
Nos sistemas lineares a saída correspondente a soma de duas entradas é igual a soma das saídas correspondentes a cada entrada individual.
Esta propriedade pode ser resumida da seguinte forma:
Nos sistemas lineares a saída é proporcional a entrada.
Compartilhe e deixe sua sugestão!
Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!
Veja a lista de posts do Curso Circuitos Elétricos.