A resposta forçada de um circuito RL é a resposta a presença de uma fonte, com condições iniciais nulas.
Veremos como determinar a equação diferencial que representa o circuito RL com fonte e, a partir dela, obter a resposta forçada em conjunto com a resposta natural, ou seja, obteremos a resposta completa do circuito.
Veja a lista de posts do Curso Circuitos Elétricos em sequência.
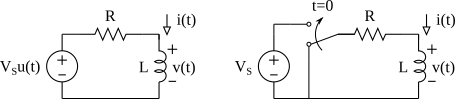
Resposta ao degrau do um circuito RL
Para determinar a resposta ao degrau de um circuito RL basta encontrar três informações:
- A corrente inicial do indutor I0=i(0);
- A corrente final do indutor I1=i(+∞); e
- A constante de tempo τ=L/R.
A resposta do degrau do circuito RL, para t>0, será a seguinte.
i(t) = I1 – (I1 – I0) e-t/τ
Determinando a equação diferencial
Vejamos agora como determinar a equação diferencial do circuito RL com fonte e em seguida como resolver ela.

Do circuito RL acima, estamos interessados na corrente no indutor i(t).
Aplicando a Lei de Kirchhoff das Tensões obtemos a seguinte equação, onde vS é a tensão da fonte, vR é a tensão no resistor e v é a tensão no indutor.
vS – vR – v = 0
As tensões nos elementos são dadas pelas seguintes equações.
v = L di/dt
vR = Ri
Substituindo obtemos a equação diferencial do circuito.
di/dt + iR/L = vS/L
Note o termo da direita que relaciona a fonte de tensão e veja que fazendo vS=0 obtemos o mesmo circuito e a mesma equação diferencial para o caso da resposta natural (sem fonte).
Resolvendo a equação diferencial
Esta equação diferencial é mais complexa que no caso da resposta natural, sendo difícil resolvê-la por inspeção. Agora utilizaremos uma técnica de resolução de equações de primeira ordem, que consiste em transformar o lado esquerdo da equação diferencial em uma derivada de uma multiplicação de duas funções.
di/dt + iR/L = vS/L
Multiplicamos a equação diferencial por uma exponencial.
eatdi/dt + eatiR/L = eatvS/L
Esta exponencial deve fazer os termos da esquerda ser uma derivada de uma função eatφ(t). Pela regra da diferenciação de uma multiplicação obtemos o seguinte.
d{eat φ(t)}/dt = eatdφ(t)/dt + aeatφ(t)
Comparando esta equação com a anterior podemos ver que φ(t)=i(t) e que a=R/L. Dessa forma temos o seguinte, com τ=L/R.
d{i(t)et/τ}/dt = (1/L) et/τ vS(t)
Integrando esta equação, com limites de -∞ a t, e multiplicando por e-t/τ obtemos a resposta do circuito RL forçada pela fonte vS(t), onde τ=L/R é a constante de tempo.
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt
Resposta completa
Sabemos que a resposta natural de um sistema é a resposta a condições iniciais, sem fontes de excitação externa.
inatural(t) = IOe-t/τu(t)
Sabemos também que a resposta forçada de um sistema é a resposta a fontes de excitação externa, sem condições iniciais.
iforçada(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt
A resposta completa de um sistema é a resposta do sistema a ambas situações, onde temos tanto a fonte de excitação externa quanto uma condição inicial.
Em sistemas lineares podemos determinar a resposta completa a partir do princípio da superposição, somando as respostas forçada e natural.
i(t) = iforçada(t) + inatural(t)
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt + IOe-t/τu(t)
Note que considerar condições iniciais IO=i(0) faz sentido apenas quando vS(t) é nula para t<0.
Obtendo a resposta ao degrau
Para obter a resposta ao degrau, basta utilizar a equação anterior e substituir vS(t)=VSu(t).
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) ∫-∞t et/τ{VSu(t)} dt + IOe-t/τu(t)
A constante VS pode sair da integral. Como u(t)=0 para t<0, podemos extrair ela para fora da integral e alterar o limite de integração inferior para 0.
i(t) = (e–t/τ/L) VSu(t) ∫0t et/τ dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) (L/R) [et/τ]0t + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) (L/R) [et/τ – 1] + IOe-t/τu(t)
i(t) = (e–t/τ/R) VSu(t) [et/τ – 1] + IOe-t/τu(t)
i(t) = (VS/R)e–t/τu(t) [et/τ – 1] + IOe-t/τu(t)
i(t) = ISu(t) – ISe–t/τu(t) + IOe-t/τu(t)
Nesta equação, onde IS=VS/R, podemos ver claramente a divisão entre a resposta forçada e a resposta natural.
i(t) = ISu(t) + (IO – IS)e–t/τu(t)
Já nesta equação podemos ver claramente a divisão entre a resposta de regime permanente e a resposta transitória.
Obtendo a resposta ao impulso
Para obter a resposta ao impulso, basta substituir vS(t)=.
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) ∫-∞t et/τ{VSδ(t)} dt + IOe-t/τu(t)
Como δ(t)=0 para t≠0, podemos substituir et/τ =1 (valor em t=0). A integral do impulso é o degrau.
i(t) = (e–t/τ/L) VS ∫-∞t δ(t) dt + IOe-t/τu(t)
i(t) = (VS/L)e–t/τu(t) + IOe-t/τu(t)
Nesta equação podemos ver claramente a divisão entre a resposta forçada e a resposta natural.
O impulso VSδ(t) gera um aumento de corrente instantâneo de amplitude VS/L no indutor. A corrente do indutor decai como na resposta natural.
i(t) = (VS/L + IO)e–t/τu(t)
Já nesta equação podemos ver que a resposta é completamente transitória, ou seja, a resposta de regime permanente é nula.
Obtendo a resposta a rampa
Para obter a resposta a rampa, basta substituir vS(t)=VSr(t)=VStu(t).
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) ∫-∞t et/τ{VStu(t)} dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) ∫0t tet/τ dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) [τet/τ(t–τ)]0t + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) [τet/τ(t–τ) + τ2] + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) (L/R) [et/τ(t–τ) + τ] + IOe-t/τu(t)
i(t) = (VS/R)e–t/τu(t) [et/τ(t–τ) + τ] + IOe-t/τu(t)
i(t) = IS(t–τ)u(t) + ISτe-t/τu(t) + IOe-t/τu(t)
Nesta equação, onde IS= VS/R, podemos ver claramente a divisão entre a resposta forçada e a resposta natural.
i(t) = IS(t–τ)u(t) + (ISτ+IO)e-t/τu(t)
Já nesta equação podemos ver claramente a divisão entre a resposta de regime permanente e a resposta transitória.
i(t) = Ist u(t) – Isτ u(t) + (ISτ+IO)e-t/τu(t)
Separando a resposta de regime permanente podemos ver ainda que a resposta completa possui três partes: uma rampa, um degrau e uma exponencial. O degrau é chamado de erro em regime permanente.
Obtendo a resposta a exponencial
Para obter a resposta a exponencial, basta substituir vS(t)=VSe-t/αu(t). Note que assumimos α≠τ; tende obter a resposta para α=τ.
i(t) = (e–t/τ/L) ∫-∞t et/τvS(t) dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) ∫-∞t et/τ{VSe-t/αu(t)} dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) ∫0t et(1/τ-1/α) dt + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) [ατ/(α–τ)] [et(1/τ-1/α)]0t + IOe-t/τu(t)
i(t) = (e–t/τ/L) VSu(t) [ατ/(α–τ)] [et(1/τ-1/α) – 1] + IOe-t/τu(t)
i(t) = (VS/R)[α/(α–τ)]e–t/τu(t) [et(1/τ-1/α) – 1] + IOe-t/τu(t)
i(t) = IS[α/(α–τ)][e-t/α – e–t/τ] u(t) + IOe-t/τu(t)
Nesta equação, onde IS=VS/R, podemos ver claramente a divisão entre a resposta forçada e a resposta natural.
i(t) = IS[α/(α–τ)]e-t/αu(t) + (IO – IS[α/(α–τ)])e-t/τu(t)
Já nesta equação podemos ver claramente a divisão entre a resposta de regime permanente e a resposta transitória.
Compartilhe e deixe sua sugestão!
Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!
Veja a lista de posts do Curso Circuitos Elétricos.