Neste post vemos como realizar a análise de malhas em um circuito resistivo. A análise de malhas é um método de análise de circuitos elétricos que utiliza a Lei de Kirchhoff das tensões para determinar correntes de malha do circuito.
Veja a lista de posts do Curso Circuitos Elétricos em sequência.
Introdução
Neste post veremos como realizar a análise de malhas para resolver circuito elétricos resistivos. A análise de malhas utiliza a Lei de Kirchhoff das tensões (LKT) para determinar as correntes de malha do circuito elétrico.
As malhas utilizadas na análise de malha são caminhos fechados no circuito que não possuem malhas internas. Isso fica claro com o exemplo.
Análise de malhas
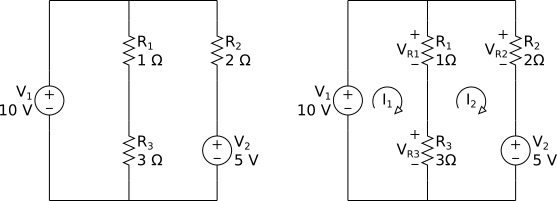
A análise de malhas é mais simples quando consideramos apenas fontes de tensão. Este é o primeiro caso que trataremos. Para exemplificar vamos utilizar o circuito abaixo.

O primeiro passo é identificar as malhas do circuito. Nenhuma malha pode conter outra malha dentro dela; por exemplo a malha que passa pela fonte de 10 V e pela fonte de 5 V não pode ser usada, pois possui duas “sub-malhas” dentro dela.
Cada malha terá sua corrente de malha. Dê um nome para cada corrente de malha, por exemplo I1, I2, I3… Tome cuidado para não repetir os nomes de fontes de corrente no circuito.
Note que a corrente que no ramo central (com dois resistores) as correntes de malha se subtraem. Dessa forma a equação da corrente resultante no ramo central é IR1=IR2=I1-I2.
O segundo passo é aplicar a Lei de Kirchhoff das tensões (LKT) em cada malha. Isso nos fornece equações que relacionam as tensões em cada um dos componentes.
VR1+VR3 = 10
VR3+VR1-VR2 = 5
O terceiro passo é determinar equações para as tensões nos componentes que dependem das correntes de malha. Para isso usamos a Lei de Ohm.
VR1 = I1-I2
VR2 = 2I2
VR3 = 3I1-3I2
O quarto passo, substituímos as equações das tensões nas equações das malhas.
(I1-I2)+(3I1-3I2) = 10
(3I1-3I2)+(I1-I2)-(2I2) = 5
Rearranjamos as equações para formar um sistema de equações com as correntes de malha como incógnitas.
4I1-4I2 = 10
4I1-6I2 = 5
Agora basta resolvermos o sistema de equações para obtermos as tensões nodais.
I1 = 5 A
I2 = 2.5 A
E este é o fim da análise de malhas, pois calculamos as correntes de malha do circuito.
Podemos agora calcular as correntes nos componentes a partir das correntes de malha.
Podemos também conferir os resultados verificando se as tensões nos componentes satisfazem a LKT, cujas equações estão no terceiro passo.
Fontes de corrente em uma malha
Vamos tratar agora da análise de malhas com fontes de corrente que pertencem a apenas uma malha. Para exemplificar vamos utilizar o circuito abaixo, onde substituímos a fonte de tensão de 5 V por uma fonte de corrente de 2.5 A, que deve nos dar o mesmo resultado.
Os passos são praticamente os mesmos.
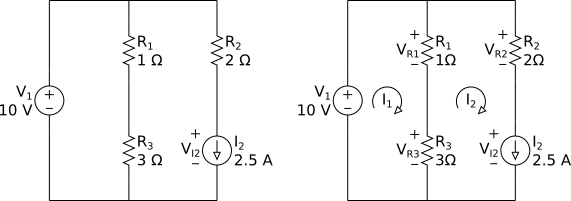
O primeiro passo é idêntico. Determinamos as malhas e damos nomes para as correntes de malha I1, I2, I3…
O segundo passo também é idêntico. Usamos a LKT em cada malha para determinar a relação das tensões nos componentes.
VR1+VR3 = 10
VR3+VR1-VR2+VI2 = 0
Veja que não temos como determinar a tensão VI2 na fonte de corrente I2. Deixemos ela como uma incógnita adicional.
O terceiro passo também é idêntico. Usamos a Lei de Ohm para determinar as equações das tensões a partir das correntes de malha.
VR1 = I1-I2
VR2 = 2I2
VR3 = 3I1-3I2
O quarto passo também é idêntico. Substituímos as equações das tensões nas equações das malhas.
4I1-4I2 = 10
4I1-6I2 = VI2
Note que agora temos duas equações e três incógnitas I1, I2, VI2.
Como na análise nodal, temos uma saída! Olhe o circuito elétrico e veja a relação que I2 tem com a fonte de corrente. Ainda por cima dei o mesmo nome para ambas!
Nesse caso também temos duas opções para análise de malhas:
- Podemos substituir o valor de I2 nas equações
- Ou podemos substituir a equação com VI2 pela equação 0I1+I2=2.5 A
Então basta resolver o sistema de equações para obter as correntes de malha.
I1 = 5 A
I2 = 2.5 A
Fontes de corrente em duas malhas
Vamos tratar agora da análise de malhas com fontes de corrente que pertencem a duas malhas. Para exemplificar vamos utilizar o circuito abaixo, onde substituímos o resistor de 1 Ω por uma fonte de corrente de 2.5 A, que deve nos dar o mesmo resultado.
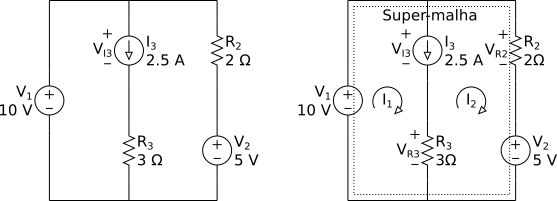
Aqui podemos fazer o mesmo procedimento anterior. Vamos obter duas equações com três incógnitas e a tensão VI3 na fonte de corrente I3 aparece nas duas equações. Isolando VI3 em uma equação e substituindo na outra ficamos com apenas uma equação e duas incógnitas.
Podemos evitar que VI3 apareça nas equações utilizando a LKT em uma super-malha que inclui as duas malhas que a fonte de corrente pertence, ignorando o ramo da fonte de corrente.
10-VR2-5 = 0
Usando a Lei de Ohm para obter as tensões nos componentes obtemos a equação a seguir.
0I1+2I2 = 5
Novamente temos uma equação e duas incógnitas. Mas lembre que a fonte de corrente I3 no ramo central define uma relação entre as correntes de malha I1 e I2. Com isso obtemos que I1-I2=I3
2I2 = 5
I1-I2 = 2.5
Então basta resolver o sistema de equações para obter as correntes de malha.
I1 = 5 A
I2 = 2.5 A
Revisão
A análise de malhas é mais simples quando temos apenas fontes de tensão.
Quando temos fontes de corrente no circuito, não conseguimos obter uma equação para determinar a tensão dessa fonte a partir da Lei de Ohm.
Se a fonte de corrente está presente em apenas uma das malhas do circuito, podemos considerar a corrente daquela malha como sendo o valor da fonte de corrente. Isso nos dá uma equação a mais (ou elimina uma variável do sistema).
Já se a fonte de corrente está presente em duas malhas do circuito, criamos uma super-malha com as malhas que esta fonte pertence, deforma que o ramo dessa fonte esteja dentro da super-malha. Essa super-malha elimina das equações a tensão da fonte de corrente. Assim ficamos com menos equações do que variáveis, o que pode ser contornado considerando que a diferença entre as correntes das duas malhas é a própria corrente da fonte.
Compartilhe e deixe sua sugestão!
Gostou do post? Foi útil? Clique abaixo e compartilhe com seus amigos!
Veja a lista de posts do Curso Circuitos Elétricos.